摘要
本篇文章描述了一个安全版本的 Yannakakis 算法(用于计算自由连接聚合查询)。本协议可用于有两方参与的安全计算模型(2PC),对比当前最先进的基于混淆电路的协议有显著的提升。
1. 介绍
当前的许多框架如 SMCQL 等,它们的中间结果可能会过大,而如此大规模的电路(混淆电路)计算起来是非常耗时的,为了改进这一点,本文提出了 secure Yannakakis 协议。
如果一个协议要忽略输入数据,它的成本就不能依赖于输入,这意味着每个输入都应该产生与最坏情况输入相同的成本,而这使得所有基于成本的查询优化技术都不会起作用。本文作者提出应该寻找最坏情况下的有效算法,无论输入是什么,其成本都是有界的,而 Yannakakis 算法正式这样一种算法,这也是作者选择将 Yannakakis 移植到 SMC 下的原因。
将 Yannakakis 移植到 SMC 下有几个技术难点:
- Yannakakis 不是基于电路的算法,而且其重度依赖于哈希连接来实现最佳的 $ O(IN + OUT) $ 的时间复杂度。为解决次问题,文章设计了一个不基于电路的用于连接和半连接的协议,其成本与输入大小加输出大小呈线性关系
- 必须将不同关系的运算符的协议放在一起,并且中间结果不能泄露任何隐私信息。为了解决此问题,文章在设计半连接协议时使用了一种“电路友好”的最新的 PSI(Private Set Intersection,隐私集合求交)协议
最终,作者将秘密共享和不经意拓展置换作为“胶水”,将上述几个部分“粘”在一起,组成了 secure Yannakakis 协议。
2. 相关工作
本章介绍了前人的一些工作:
- 基于 Sharemind 实现的用于安全计算双向连接的不经意 AES 协议,但是此协议由于揭露了中间连接的大小而无法做到与其他运算符相结合
- 通过提供一个可信的第三方来进行计算(当前有许多硬件芯片如 Intel SGX 等可作为一个信任方),本文的协议是基于无信任参与方的,但是也可以将一些计算移动到信任方(如果有)
- 外源数据库如 CryptDB 和 Cipherbase 等,数据拥有者将数据加密后上传到外源数据库,外源数据库为数据拥有者提供 SQL 服务,但是这与 SMC 模型中大多数数据拥有者希望在不共享数据的情况下进行查询的想法不同
3. 附加说明关系的连接聚合查询
本章描述了查询定义和 Yannakakis 算法

将查询属性作为点,关系作为边,可将查询转换为一个超图,再将超图转换为连接树(连接树不是唯一的)(join tree)。上图是如下SQL查询
SELECT B, D, E, F, SUM(D+F*G)
FROM R1 JOIN R2 JOIN R3 JOIN R4 JOIN R5
GROUP BY B, D, E, F的连接树,其中有下划线的代表是要输出的属性(B,D,E,F),而 free-connex 是指所有的输出属性都在不输出属性的上方(parents)。如左边 (a) 树,未输出的属性 A 在输出的属性 B 和 D 的上方,所以这棵树就不是 free-connex 的,而 (b) 树中所有输出的属性都在未输出的属性上方,所以这棵树就是 free-connex 的。对于所有 free-connex 的连接树,Yannakakis 算法都可以做到 $ O(IN + OUT) $。
Yannakakis 算法
注意:Yannakakis 应用于 free-connex 的连接树(无环查询)
修改后的 Yannakakis 算法主要有以下三个步骤:
- 减少,通过将孩子投影到其父亲来消除不输出的属性,如上图中 (b) 树 可以将 R2 投影到 R1 来消除不输出的属性 C
- 半连接,当消除不输出属性后将孩子与父亲进行半连接来消除无用的行,如将 R1 与投影后的 R2 进行半连接,并用结果取代 R1,并删除 R2
- 全连接,当所有前置操作都结束后,从下至上进行全连接,并输出结果
Yannakakis 有两个阶段,一个是 semijoin 半连接,另一个是 join-aggregate 连接聚合阶段,而 Secure Yannakakis 将连接聚合阶段分为了减少阶段和全连接阶段,并将减少阶段置于半连接阶段之前,这并不会影响 Yannakakis 的正确性证明。
修改后的 Yannakakis 仍然是 $ O(IN + OUT) $ 的复杂度
4. 安全查询评估
本章主要讲述了 Secure Yannakakis 的安全性。
文章引入了真实-理想世界范式,在理想世界中,Alice 和 Bob 将他们的数据发送给受信任的第三方,第三方评估查询,并将结果返回给Alice(指定的接收者),Bob没有得到任何输出。;在现实世界中,他们遵循规定的协议来评估查询。一方的视图(在理想和现实世界中)由她/他在协议期间发送和接收的所有消息,加上她/他自己的输入和输出组成。如果对于现实世界中的任何输入和任何对手 A,存在一个模拟器,使得给定 A 的理想世界视图,模拟器可以产生一个与A的现实世界视图无法区分的视图,则该协议是安全的。
当参与双方的视图之间的统计距离小于 $ 2^{- \sigma} $ 时称他们是不可区分的(其中 $ \sigma $ 为安全参数)
对于计算不可区分性,文章将是视图输入到一个概率多项式时间的区分器,由它来试图决定这是个真实世界视图还是一个模拟视图,要求成功概率不超过 $ \frac{1}{2} + 2_{- \sigma} $,计算不可区分性通常基于对某些问题的严格假设,如伪随机函数、离散对数和整数分解。计算安全参数是指密码原语中用于实现计算不可区分性的密钥长度。
最后,协议也被允许失败,即它在没有计算正确输出的情况下终止。此概率也设置为 $ 2^{- \sigma} $ ,与违反安全性的概率相同。
5. 密码原语
本章主要讲述了 Secure Yannakakis 所使用的一些密码学技术(秘密共享,混淆电路,隐私集合求交(PSI),不经意扩展置换(OEP)和在秘密共享载荷上的隐私集合求交)
上述技术中 秘密共享 和 混淆电路 已做过笔记,在此处不再赘述
Secure Yannakakis 使用算数共享,布尔混淆电路,基于布谷鸟哈希和混淆电路的PSI协议和不经意扩展置换
6. Secure Yannakakis
本章主要讲述了 Secure Yannakakis 的具体实现。
Secure Yannakakis 中的 投影-聚合、半连接和连接协议必须满足以下要求:
- 每个输入关系由 Alice 或 Bob 拥有
- 输出关系由一方拥有,输出关系中的元组只能依赖于拥有方的输入关系和查询结果
- 输入输出关系的注释以秘密共享的形式由 Alice 和 Bob 持有
- 输出关系的大小仅取决于公开信息(输入关系大小和查询结果大小),而不是输入元组
- 每个输入和输出元组(及其注释)的访问模式无法区分
不经意投影-聚合协议
对于 $ \pi_{F}^{\oplus}(R) (select \oplus \quad (annotation) \quad group \quad by \quad F)$,Alice 先将 R 中的元组按照 F 进行排列,以保证相关的元组是相邻的,随后 Alice 和 Bob 使用不经意扩展置换来将分享的注释重新排序,这样能够让其与排序过的元组对应上,随后将其一个一个对应上即可。为保证这个算法是不经意的,使用混淆电路来进行实现。
对于 $ \pi_{F}^{1}(R) (\{ t \in R | \upsilon(t) \neq 0 \})$,因为不能够让 Alice 知道 $ \pi_{F}^{1}(R) $(它依赖于 R 的注释),所以作为替代向 Alice 发送一个语意上与 $ \pi_{F}^{1}(R) $ 相等的关系。输出包含所有在 $ \pi_{F}(R) $ 中的元组。对于在 $ \pi_{F}^{1}(R) $ 中的元组,他的注释会是 $ [\![1]\!] $,而对于其他的元组则是 $ [\![0]\!] $( $ [\![x]\!] $ 代表秘密共享形式的 $ x $)
不经意半连接协议
Secure Yannakakis 拥有两种类型的半连接,一种是一个带注释的链接 $ R = R_{F} \bowtie^{\otimes} R_{F^{'}} $,另一种是 $ R = R_{F} \ltimes^{\otimes} R_{F_{'}} $
TODO: 补充实现步骤
不经意连接协议
本协议分为三步:
-
揭露
通过对悬垂和非悬垂元组注释的假设,我们可以知道有 $ R_{F}^{*} = \pi_{F}(\mathcal{J}^{*}) $($ R^{*} $ 代表 $ R $ 中的所有注释不为 0 的元组集合),这代表了 $ R_{F}^{*} $ 是可以从 $ \mathcal{J}^{*} $ 派生出来的(但他的注释不能),所以可以被发送给 Alice。随后使用 $ |R_{F}| $ 混淆电路来检查对每个 $ t \in R_{F} $,是否有 $ \upsilon{t} = [\![\upsilon(t)]\!]_{1} + [\![\upsilon(t)]\!]_{2} = 0 $,如果结果为是,则返回一个假元组,否则返回 $ t $。如果 $ t $ 不是假的,则 Alice 将其放入 $ R_{F}^{*} $。运行和交流耗时为 $ O(IN) $ -
连接
经过上一步骤,对于任意的关系 $ R_{F} $,Alice 都知道 $ R_{F}^{*} $。她可以在本地使用无注释的 Yannakakis 算法来计算连接 $ \mathcal{J}^{*} = \bowtie_{F \in \epsilon} $,并将结果 $ OUT = |\mathcal{J}^{*}| $ 发送给 Bob。Alice 可以向 $ \mathcal{J}^{*} $ 中加入假元组并在之后向 Bob 发送 $ \mathcal{J}^{*} $ 的大小来防止 Bob 知道 $ OUT $ 的确切值。这个步骤耗时为 $ O(IN + OUT) $,但交流耗时是一个常数 -
计算注释
设 $ t_{i} $ 为 $ \mathcal{J}^{*} $ 中的第 $ i $ 个元组,对每个关系 $ R_{F} $,Alice 定义一个扩展置换:$ \xi_{F}: [OUT] \rightarrow [|R_{F}|] $,其中 $ \xi_{F}(i) = index(\pi_{F}(t_{i}) \quad in \quad R_{F}, i \in [OUT]) $。随后 Alice 和 Bob 使用 OEP 将 $ R_{F} $ 的注释进行重新排序,他们就可以知道 $ \{[\![\upsilon(\pi_{F}(t_{i}))]\!]\} $,最后,对每个 $ t_{i} \in \mathcal{J_{*}} $。最终,他们使用混淆电路计算注释 $ [\![\upsilon(t_{i})]\!] = [\![\otimes_{F \in \epsilon} \upsilon(\pi_{F}(t_{i})) ]\!] $。此步骤耗时为 $ O(IN + OUT) $
Secure Yannakakis 算法
Secure Yannakakis 算法的描述如下:
-
减少阶段
在本步骤中,算法自下向上遍历连接树 $ \mathcal{T} $,同时当 $ F^{'} \subseteq F_{p} $ 时执行更新 $ R_{F_{p}} \leftarrow R_{F_{p}} $,而这可以进一步分解为两步:计算 $ \pi_{F^{'}}^{\oplus}(R_{F}) $ 和半连接,前者通过不经意投影-聚合协议计算,后者通过不经意半连接协议计算。协议智慧更改其注释,并不会修改 $ R_{F_{p}} $ 的大小。此阶段消耗为 $ O(IN) $。 -
半连接阶段
原始的 Yannakakis 算法通过两次半连接来删除所有的悬垂元组,但他不是不经意的。修改后的 Yannakakis 算法通过将它们的注释设为0来代替这个操作,可以通过不经意半连接协议进行计算。此阶段的消耗也是 $ O(IN)$。 -
全连接阶段
在前两个阶段后,只剩下输出属性,悬空元组的注释都是0。通过使用不经意连接协议可以计算出全连接的结果 $ \mathcal{J}^{*} $。因为 $ \mathcal{J}^{*} $ 的注释世界过的一部分,所以这些可以揭露给 Alice。此阶段的消耗为 $ O(IN + OUT) $
优化
-
当一方拥有一个关系和其注释时
在这种情况下,带注释的投影聚合协议可以直接在本地计算。在不经意半连接协议中,当 Bob 知道所有自己所知道的关系的注释的时候,他们只需要带有有效负载的 PSI 协议,而不需要运行带有秘密共享的 PSI 协议。这种优化通常只在 Yannakakis 协议开始时有效,因为对于每个协议,输出关系的注释都将变成共享形式。 -
当一方拥有一个包含根节点的子树
假设 Alice 拥有包含根节点的子树。在 Yannakakis 算法自下向上的减少阶段中,对 Bob 的所有关系,全部计算都在本地完成,然后它们执行一些不经意半连接,其中 Bob 知道所有关于他所拥有的关系的注释,所以我们只需要使用带有有效负载的 PSI 协议。之后,即使注释是共享的,所有计算都是在 Alice 的关系上进行的。因此我们只需要简化的不经意半连接协议。在这种特殊类型的查询中,我们不需要使用带有秘密共享有效负载协议的PSI,因此可以提高效率。
7. 扩展
- 选择条件
假设此时对每一个关系 $ R_{F} $ 有一个条件限制 $ \phi_{F} $,对于不同的隐私要求,有以下几种选项:
- 条件的选择性不是私有的,则直接将 $ R_{F} $ 替换为 $ \sigma_{\phi_{F}}(R_{F}) $,这样可以降低一些算法的消耗
- 条件的选择性是私有的,则将所有不符合 $ \phi_{F} $ 的元组都替换为假元组后运行 Secure Yannakakis 算法
- 如果精确的选择性是私有的,但是可以透露一些上限,则可以将 $ R_{F} $ 替换为 $ \sigma_{\phi_{F}}(R_{F}) $,随后添加一些假元组。这在成本和隐私之间取得了很好的平衡
-
查询组合
有些聚合查询可能不是 free-connex 的,但是他们可以分解为两个或多个这样的查询。对此我们首先运行 Secure Yannakakis 算法的两个实例来计算每个类的共享形式的计数和总和。然后,我们为每个类使用混淆电路来计算平均值,并且只向 Alice 透露平均值。 -
针对查询结果保护隐私
根据本文定义的 2PC 模型,Alice 可以知道查询的结果,当查询结果是敏感的时候,可以使用拉普拉斯分布向结果中加入噪声,并通过混淆电路并入结果发送给 Alice。
8. 实验
经过试验可以发现 Secure Yannakakis 在速度上有着难以置信的提升,下面是一些图表


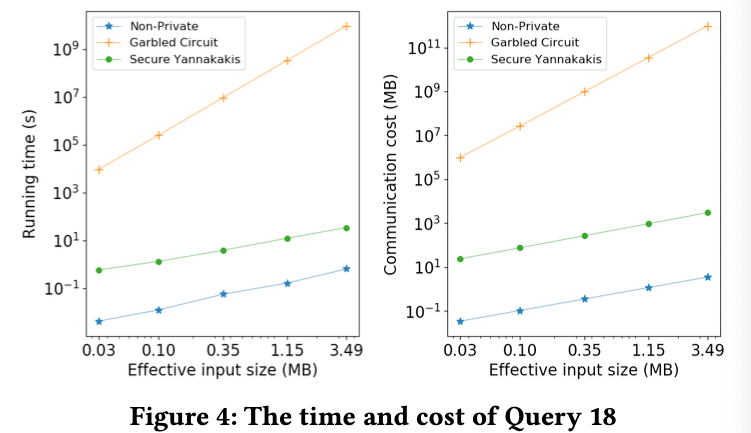


不错