隐私保护算法：K-Anonymity、L-Diversity 和 T-Closeness

背景

未经脱敏的数据在公布后可能会被一些攻击者逆向得到用户的隐私信息，所以在发布前进行数据脱敏是很有必要的，而简单的脱敏并不能阻止攻击者获取隐私信息

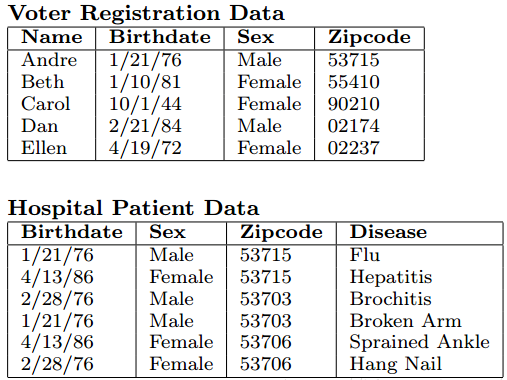
如上表，医院发布的数据（Hospital Patient Data）中已经抹去了姓名、身份证号等信息，但是攻击者如果知道上面的投票表（Voter Registration Data）就可以通过生日（Birthdate）、性别（Sex）和邮编（ZIPcode）来推测出 Andre 患有流感（Flu），这被称作连接攻击，通过某些属性与外部表进行连接获取隐私数据

K-Anonymity（K-匿名）

为了解决上述连接攻击的情况，K-匿名应运而生。K-匿名的基本思想是对同一个准标识符（可以和外部表链接来识别个体的最小属性集，如上述例子中的 { 生日，性别，邮编 } ）至少要有 $ k $ 条记录，这样攻击者就不能通过连接来获取隐私信息了。

Table 1. Original Patients Table

Table 2. A 3-Anonymous Version of Table 1

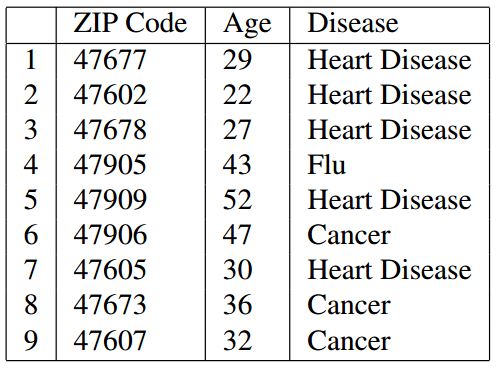
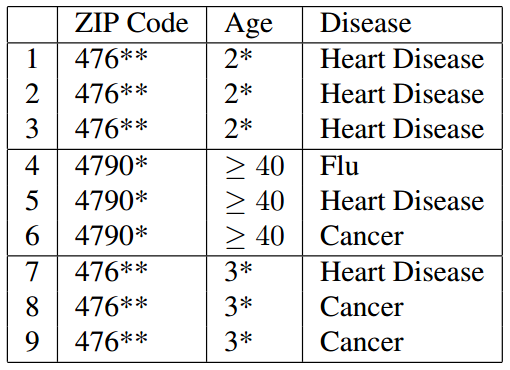
我们可以看到，在经过K-匿名处理后（例子中为3-匿名）已经不能通过连接攻击来获得用户隐私了，因为连接后有多个结果，攻击者不能确定唯一的一条结果。

但是K-匿名也有缺点，如 Table 2 所示，脱敏处理后的数据出现了相同项，也就是说，只要攻击者知道表中某一用户的邮编以 476** 开头，并且年龄在20多岁，就可以确定他患有心脏病（Heart Disease），这被称为同质化攻击。同时，如果攻击者知道一些关于用户的背景也有可能能获取到隐私，加入攻击者知道 A 的邮编为 476**，年龄为30多岁，并且患心脏病的概率很低，那么从 Table 2 的 789 列就可以推测出 A 患了癌症（Cancer），而这被称为背景攻击

L-Diversity（L-多样性）

为了解决K-匿名无法防范同质化攻击和背景攻击的情况，L-多样性出现了。-多样性在K-匿名的基础上对每个等价类都保证敏感属性至少有 $ l $ 个取值，使得攻击者最多以 $ \frac{1}{L} $ 的概率确认某个体的敏感信息，如下图就满足 3-diversity

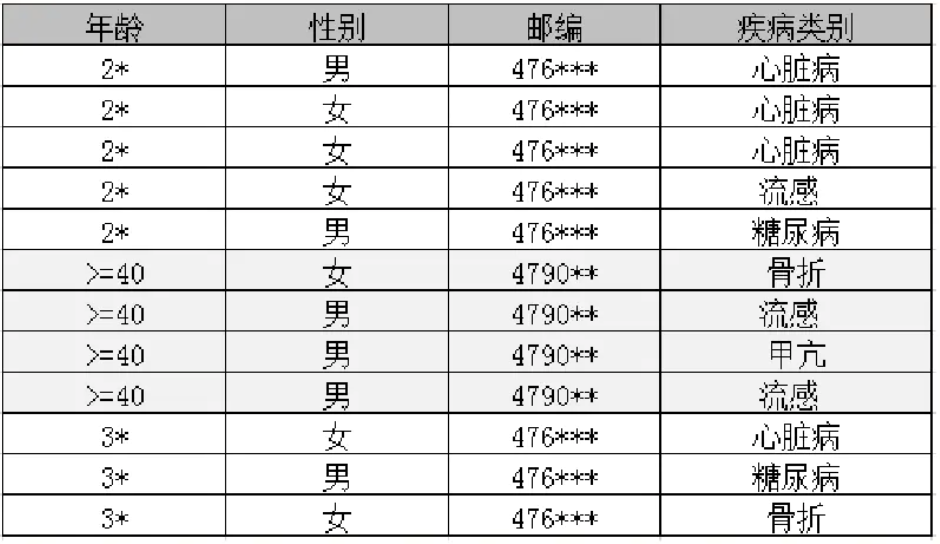
l-diversity 有多种表示方法：

• 可区分良表示（Distinct l-diversity）：同一等价类中敏感属性至少有 $ l $ 个可区分的取值， 但是如果某一个值的频率明显高于其他取值则可能让观察者以较高的置信度认为此等价类中的敏感属性都是这个值
• 熵良表示（Entropy l-diversity）：记 $ S $ 为敏感属性的取值集合，$ p(E, s) $ 为等价类 $ E $ 中敏感属性取值 $ s $ 的概率，Entropy l-diversity 要求 $ Entropy(E) = -\sum_{s \in S}logp(E, s) \geq log l $
• 递归良表示（Recursive(c, l)-Diversity）：如果等价类的敏感属性有 $ m $ 中取值，记 $ r_i $ 为出现次数第 $ i $ 多的取值的频次，如果等价类满足 $ r_1 < c(r_l + r_{l+1} + \dots + r_m) $，责成等价类具有 Recursive(c, l)-diversity

L-Diversity 也有一些缺点，一方面，L-Diversity 可能难以实现且没有必要实现，另一方面，我们考虑疾病检验报告的例子，我们假设整体阳性率为1%，一种情况是一个等价类里恰好有一半阳性，一半阴性，此时相比整体1%阳性的概率，该等价类中每个个体都有 $ \frac{1}{2} $ 的概率被认为是阳性。再考虑另一种情况，49个阳性和1个阴性，在该等价类中每个个体都有98%的概率被认为是阳性，远高于整体的1%，而这两种情况都代表了一种很严重的隐私风险，这种攻击被称为偏斜攻击（Skewness Attack）。另外一种对 l-diversity 有影响的攻击是相似度攻击（Similarity Attack），如果敏感属性是工资，在某一等价类中的取值都在 3k-5k 之间，那么观察者只要知道用户在这一等价类中就可以知道其工资处于较低水平，而具体数值观察者并不关心。

T-Closeness（T-相近）

T-相近是L-多样性的进一步细化。T-相近要求每个K-匿名组中敏感属性值的统计分布与该属性在整个数据集中的总体分布“接近”。

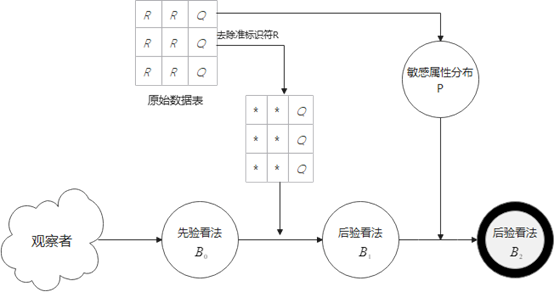
我们假设观察者对个体的敏感看法有一先验看法 $ B_0 $，给观察者一个抹去准标识符信息的数据表，其中敏感属性的分布为 $ Q $，根据 $ Q $，观察者的先验概率变成 $ B_1 $。最后，发布含有准标识符信息的数据表，个体所在等价类的敏感属性的分布为 $ P $，则根据 $ P $，观察者的看法变为 $ B_2 $。
L-Diversity 的思想是限制 $ B_0 $ 和 $ B_2 $ 之间的差异，而 T-Closeness 的思想是限制 $ B_1 $ 和 $ B_2 $ 之间的差异。T-Closeness 通过限制 $ P $ 和 $ Q $ 之间的距离来限制从 $B_1$ 到 $ B_2 $ 的增益。直觉上来说，如果$ P = Q $，那么 $ B_1 $ 和 $ B_2 $ 应该是相同的。如果 $ P $ 和 $ Q $ 很接近，那么 $ B_1 $ 和 $ B_2 $ 也应该很接近，即使可能与 $ B_0 $ 有很大不同。若一个等价类的敏感属性取值分布与整张表中该敏感属性的取值分布的距离不超过阈值t，则称该等价类具有t-相近性。若一个表中所有等价类都有t-相近性，则该表也有t-相近性。
对于 $ P $ 和 $ Q $ 之间的距离，$ P $、$ Q $ 为两个概率分布 $ P = (p_1, p_2, \dots, p_m) $ 和 $ Q = (q_1, q_2, \dots, q_m) $，众所周知的变量距离公式是 $ D[P,Q] = \sum_{i=1}^{m}\frac{1}{2}|p_i - q_i| $，然而这个公式并不能反映值之间的语义距离。所以我们使用 EMD（Earth Mover's Distance，陆地移动距离）来衡量他们之间的距离。我们设 $ r_i = p_i - q_i $，EMD 可以如下计算：$ D[P, Q] = \frac{1}{m - 1}(|r_1| + |r_1 + r_2| + \dots + |r_1 + r_2 + \dots + r_{m - 1}|) = \frac{1}{m-1}\sum_{i=1}^{m}|\sum_{j=1}^{i}r_j| $

T-相近性可以防止属性泄露，但是不能防止身份泄露，所以有时候可能同时需要K-匿名与T-相近性。此外，T-相近性对于针对K-匿名算法的同质化攻击和背景攻击并不能保证永远不会发生，而是保证了如果这类攻击发生在了此类表中，那么即使使用完全广义的表也能发生相似的攻击。所以如果要发布数据，使用T-相近性进行脱敏是最好的。

参考文献

• Li, N.; Li, T.; Venkatasubramanian, S. t-closeness: Privacy beyond k-anonymity and l-diversity. In Proceedings of the IEEE International Conference on Data Engineering, Istanbul, Turkey, 15–20 April 2007;