摘要
本文引入了 OpBoost 框架,提出了三种在垂直联邦学习下的满足基于距离的 LDP(dLDP)的保序脱敏提升树算法用于对训练数据进行脱敏,优化了 dLDP 定义,并研究了有效的采样分布进一步提高了算法的精度和效率。
介绍
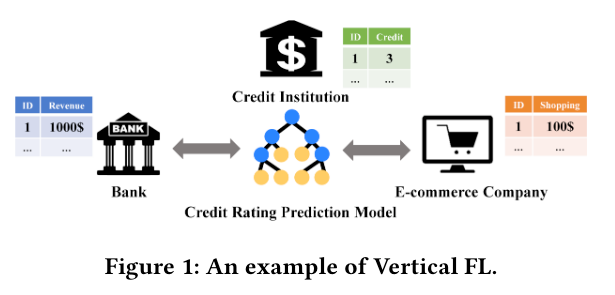
本章介绍了一些基础概念,如联邦学习,HFL,VFL,提升树等
提升树算法是一种流行的监督机器学习算法,有着高效性和可解释性的特点,被广泛应用于基于异构特征的预测任务中,但是当前现有的大多数提升树算法都是在集中式设置下提升的,直接访问整个数据集,在当前人们越来越注重隐私的环境下集中式的设置限制了提升树算法的广泛部署,所以设计一个使用的隐私保护VFL提升树算法成为一个重要问题。
本文贡献如下:
- 提出了新的隐私保护垂直联合提升树框架 OpBoost
- 设计了三种保序脱敏算法
- 优化 dLDP 定义
- 引入新的保序度量用于量化保序脱敏算法的隐私性,并使用此度量对 OpBoost 进行了综合评估
一些知识
基于距离的本地差分隐私(Distance-based Local Differential Privacy, dLDP)
对任意输入 $ x, x^\prime \in \mathbb{D} $ 和 $ \left| x - x^\prime \right| \leq t $,对所有 $ y \in \operatorname{Range} (\mathcal{M}) $ 有
$$ \operatorname{Pr}[\mathcal{M}(x)=y] \leq e^{t \epsilon} \cdot \operatorname{Pr}\left[\mathcal{M}\left(x^{\prime}\right)=y\right] $$
保序脱敏算法(Order-Preserving Desensitization Algorithm)
-
保序脱敏算法(Order-Preserving Desensitization Algorithm)
令 $ X = x_1, x_2, \dots, x_n (\forall i.x_i \in \mathbb{N}) $ 为敏感序列,$ Y = y_1, y_2, \dots, y_n (\forall i.y_i \in \mathbb{N}) $ 为由脱敏算法 $ \mathcal{R} $ 生成的噪声序列。脱敏算法 $ \mathcal{R} $ 为保序的当且仅当
$$ \begin{aligned}
& \forall i, j . x_i>x_j \Rightarrow y_i>y_j, \quad \text { and } \\
& \forall i, j \cdot y_i>y_j \Rightarrow x_i \geq x_j .
\end{aligned} $$ -
概率保序脱敏算法(Probabilistic Order-Preserving Desensitization Algorithm)
令 $ X = x_1, x_2, \dots, x_n (\forall i.x_i \in \mathbb{N}) $ 为敏感序列,$ Y = y_1, y_2, \dots, y_n (\forall i.y_i \in \mathbb{N}) $ 为由脱敏算法 $ \mathcal{R} $ 生成的噪声序列。脱敏算法 $ \mathcal{R} $ 为概率保序的当且仅当
$$ \forall i, j . x_i>x_j \Rightarrow \operatorname{Pr}\left[y_i>y_j\right] \geq \gamma(t) $$
其中 $ \gamma(t) \in [0, 1] $,$ \left| x_i - x_j \right| \leq t $。在这里 $ \gamma(t) $ 是与 $ x_i $ 到 $ x_j $ 之间的距离有关的函数,当 $ \gamma(t) = 1 $ 时则为保序脱敏算法。
梯度提升树(Gradient Tree Boosting)
GBDT (Gradient Boosting Decision Tree),中文名为梯度提升决策树,是一种基于决策树的增强学习算法,它被广泛地应用于回归、分类以及排序等问题。XGBoost 是一种 GBDT 的高效实现。
在梯度提升树的过程中,只有特征值的顺序是必要的。该算法(XGBoost)持续寻找分裂点并计算其增益。我们设 $ I_L $ 和 $ I_R $ 分别为样本集分裂(split)后的左右节点,$ g_i $ 和 $ h_i $ 为梯度,$ \lambda $ 和 $ \omega $ 为正则化参数,分裂的增益如下:
$$ G_{split}=\frac{1}{2}\left[\frac{\left(\sum_{i \in I_L} g_i\right)^2}{\sum_{i \in I_L} h_i+\lambda}+\frac{\left(\sum_{i \in I_R} g_i\right)^2}{\sum_{i \in I_R} h_i+\lambda}-\frac{\left(\sum_{i \in I} g_i\right)^2}{\sum_{i \in I} h_i+\lambda}\right]-\omega $$
计算 $ G_{split} $ 所需所有的变量都只能从特征值的顺序中推导出来。因此我们可以在不知道每个特征的确切值的情况下构建提升树。
系统概览
架构
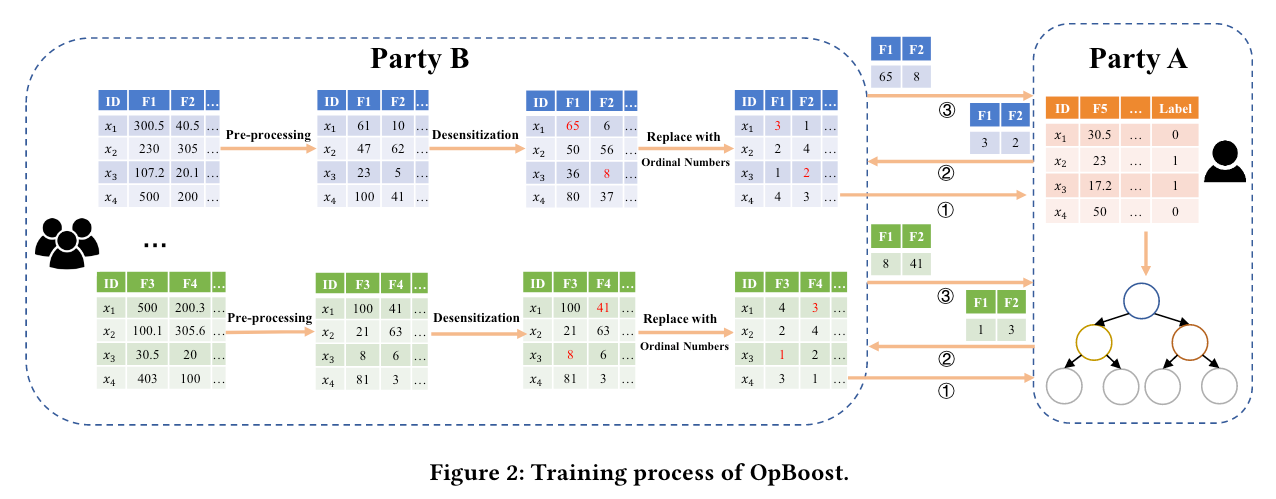
在 OpBoost 中用户被分为两类:
- A方为持有训练样本标签的用户,在训练过程中A方充当中心服务器,与B方交换信息,进行模型训练。训练好的模型只存储在A方,A方负责利用其对新样本进行预测。
- B方为仅持有样本若干特征的用户集合。B方作为客户端,通过与A方交换必要的信息来参与训练
执行流程
训练流程(Training Process)
首先B方在与A方交流前将本地特征脱敏:
- 特征值预处理
提升树算法会对具有自然排序的数值和分类特征进行不同的处理,通常采用 one-hot 编码,编码后可以使用 LDP 机制脱敏 - 用保序脱敏算法进行脱敏
- 用序号代替脱敏值后发送给A方
随后A方在收集B方的所有特征信息后找到特征上的最佳分割点(将序号记录为分割点)
最后A方将所有拆分点的序号发送给B方得到其脱敏值,并以此更新树模型
预测流程(Prediction)
在上述训练流程结束后,A方会得到一个完整的决策树模型,A方可以独立预测本地的新样本(非私有),也可以与B方合作预测新样本(私有)。所有新样本在脱敏或输入模型前都需要做与训练样本相同的处理。
特征值预处理算法(Pre-Processing for Feature Values)
该算法将所有不同特征的数值映射到一个统一的离散值域
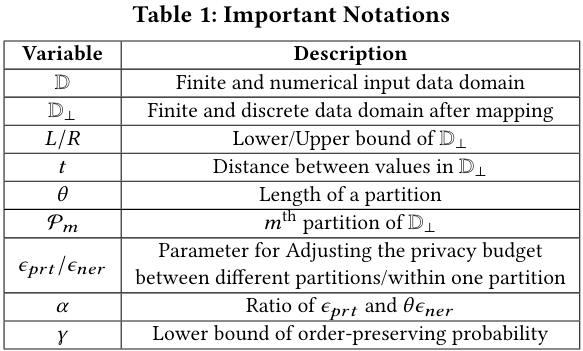
上图是一些标志的定义,算法通过应设函数 $ \mathcal{B} $ 将离散数值映射到统一离散值域 $ \mathbb{D}_\perp $。设 $ \mathcal{X}_c \in \mathbb{D} $ 为一个特征的数值集合,B方将每个值 $ \mathcal{X}_c^i $ 做如下映射:
$$ X_{i n t}^i=\left\lceil L+\frac{X_c^i-\text { lower }}{\text { upper-lower }} \cdot(R-L)\right\rceil $$
其中 $ \operatorname{lower} $ 和 $ \operatorname{upper} $ 分别是 $ \mathbb{D} $ 的上下界,$ L $ 和 $ R $ 分别为 $ \mathbb{D}_\perp $ 的上下界。映射域 $ \mathbb{D}_\perp $ 越大,原始值的顺序就可以保留更多。将不同特征的值映射到统一值域中的原因是两个属性对于数值变化的敏感程度可能不同,所以需要将其映射到统一值域以方便评估脱敏化数据集的隐私性和效用性。
保序脱敏算法(Order-preserving Desensitization Algorithms)
该算法使用了 dLDP 机制实现保序脱敏,相比于 LDP 机制,dLDP 机制使得距离近的数据更难区分,而不是任意键值对之间。这使得以此训练出来的模型具有更高的准确性和更高的性能(LDP机制使得大量顺序信息丢失)。此算法有三个部分:Global-Map,Adj-Map 和 Local-Map。
Global-Map
算法描述如下

该算法建立在指数机制的变体上,根据一个效用函数为每个值分配输出概率。效用函数可以定义为该值域敏感值之间的距离,使得某个值可以以更高的概率脱敏得到更近的值。
Adj-Map
在经过分析过后发现在对有序数值进行脱敏时基于距离来分配在值域 $ \mathbb{D}_\perp $ 中映射其他值的概率更为合适。
但是现有的 dLDP 是基于 L1 距离,并且并未考虑数据分区的问题(数值可能相差很小但却在两个分区,例如血糖大于7mmol/l可能是糖尿病,6.9和7.1仅差0.2,但是和5.0和5.2之间的0.2完全不同,因为6.9和7.1跨越了数据的分区),于是本文扩展了 dLDP 的定义,增加了一个隐私预算参数,用两个参数来调整在不同分区和相同分区内的隐私等级。扩展后的 Partition-dLDP 定义如下:
一个算法 $ \mathcal{M} $,当且仅当其对所有的输入 $ x, x^\prime \in \mathbb{D}_\perp $,$ \left| x - x^\prime \right| \leq t $,$ \mathbb{D}_\perp $ 等分为若干长度为 $ \theta $ 的划分,对任何输出 $ y \in \operatorname{Range}(\mathcal{M}) $,有
$$ \operatorname{Pr}[\mathcal{M}(x)=y] \leq e^{\left\lceil\frac{t}{\theta}\right\rceil \epsilon_{\text {prt }}+\theta \epsilon_{n e r}} \cdot \operatorname{Pr}\left[\mathcal{M}\left(x^{\prime}\right)=y\right] $$
当满足如下条件时:
$$ \left\{\begin{array}{l}
\epsilon_{p r t}=\theta \epsilon_{n e r} \\
\epsilon_{n e r}=\frac{\epsilon}{1+\theta /\left|D_{\perp}\right|}
\end{array}\right. $$
Partition-dLDP 将退化为现有的 dLDP 定义
但是 Partition-dLDP 有个局限性就是他只能应用于均匀的划分(像是分数这种0-60不及格,60-80及格,80-100优秀的就是不均匀划分),而这也是未来可以拓展的方向
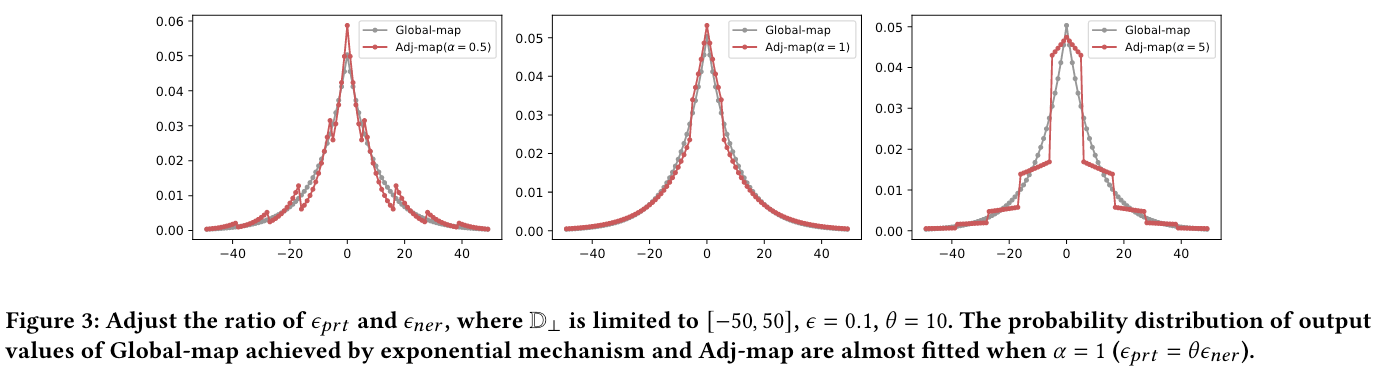
Adj-Map 算法描述如下

Adj-Map 算法首先以满足 $ \epsilon_{prt}-dLDP $ 的 Global-Map 为输出域随机选择一个分区作为输出域,随后利用满足 $ \epsilon{ner}-dLDP $ 的 Global-Map 将敏感值随机映射到该分区中的一个值
Local-Map
当 $ \epsilon_{prt} $ 增大时,敏感值可以以更大的概率映射到它所在的分区,当 $ \epsilon_{prt} = \infty $ 时,脱敏值的输出域从 $ \mathbb{D}_\perp $ 缩小到它所在的分区,因此不同分区的敏感值在脱敏后仍然保持着顺序。具体来说每个敏感值在其所在的分区通过满足 $ \epsilon_{ner}-dLDP $ 的 Global-Map 进行脱敏。划分的粒度越细,保留的顺序信息就越多。
使用有界离散拉普拉斯提高效率
由于指数机制下采样的计算复杂度和输出域的大小成正比,如果输出域较大的话采样过程就会变得很低效。并且指数机制要求输入/输出域的边界已知,在复杂场景下可能很难脱敏,如果输入域未知的情况下还要引入新的参数,这可能会对隐私有一定影响,会增加部署需求。
本章重点研究的是输入域未知或输出域较大的情况,使用有界离散拉普拉斯机制来替换指数机制。拉普拉斯分布支持无界的输入/输出采样,使得输入/输出域可以视为无穷大,下面是离散拉普拉斯分布的定义:
具有尺度参数 $ \lambda $ 的离散拉普拉斯分布记为 $ \operatorname{Lap}_{\mathbb{Z}}(\lambda) $,其中 $ \lambda = \frac{1}{\epsilon} $。其概率分布定义如下:
$$ \forall z \in \mathbb{Z}, \operatorname{Pr}[Z=z]=\frac{e^{1 / \lambda}-1}{e^{1 / \lambda}+1} \cdot e^{-|z| / \lambda} $$
由于拉普拉斯机制的输出域无界,所以就会出现值在期望输出域外的情况,对于这种情况进行重采样,重采样得到的有界离散拉普拉斯概率分布如下:
给定一个采样范围 $ [l, u] $,有界离散拉普拉斯概率分布为 $ \forall z \in[l, u], \operatorname{Pr}[Z=z]=\tau \cdot \frac{e^{1 / \lambda}-1}{e^{1 / \lambda}+1} \cdot e^{-|z| / \lambda} $,其中 $ \lambda = \frac{1}{\epsilon} $,有
$$ \tau= \begin{cases}\frac{2}{e^{u / \lambda}\left(1-e^{-(u-l+1) / \lambda}\right)}, & l<u<0 \\ \frac{2}{1-e^{-(-l+1) / \lambda}-e^{-(u+1) / \lambda}+e^{-1 / \lambda}}, & l<0<u \\ \frac{2}{e^{-l / \lambda}\left(1-e^{-(u-l+1) / \lambda}\right)}, & 0<l<u\end{cases} $$
重采样的概率随着域的减小而增大,这会导致采样的耗时增加,而对于某些具有很强的侧信道攻击能力的敌手来说有可能从中可以得到一些信息,所以当输入输出域较小时建议使用指数机制。
理论分析
一个特征值的脱敏值在排序后没有跨越任何划分点 $ x^{\dagger} \in [L, R] $ 的概率至少为 $ \beta $,其中
$$ \beta=\sum_{k \in I_l} \sum_{x^{\dagger} \in[L, R]}\left(\mathcal{M}\left(k, x^{\dagger}\right) \cdot \prod_{j \neq k, j \in I_l} \sum_{x_l \in\left[L, x^{\dagger}\right]} \mathcal{M}\left(j, x_l\right) \cdot \prod_{j \in I_r} \sum_{x_r \in\left[x^{\dagger}+1, R\right]} \mathcal{M}\left(j, x_r\right)\right) $$
$ \beta $ 的值会受到特征值的分布和密度以及划分点的位置所影响。下图是本文的保序脱敏算法与 LDP 机制的比较:
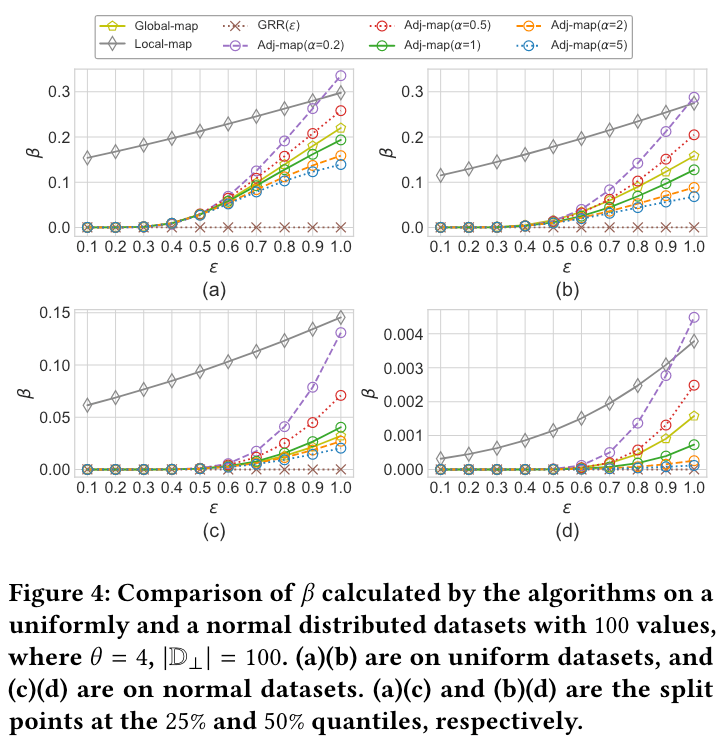
可以看到,数据集的分布越集中或越密集,脱敏后无序值对的数量越高,也就降低了脱敏后值的效用程度。此外,可以看到 $ \beta $ 随着划分点接近特征值的中位数而减小。尽管许多因素对 $ \beta $ 的影响都比较大,但本文提出的算法总是优于 LDP 方法。
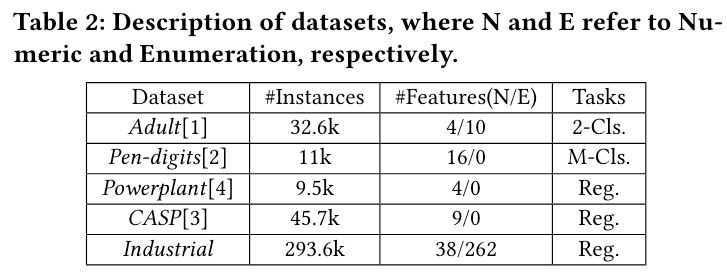
实验
本文在 Salaries 数据集下对 OpBoost 进行了评估。数据集和实验结果如下:
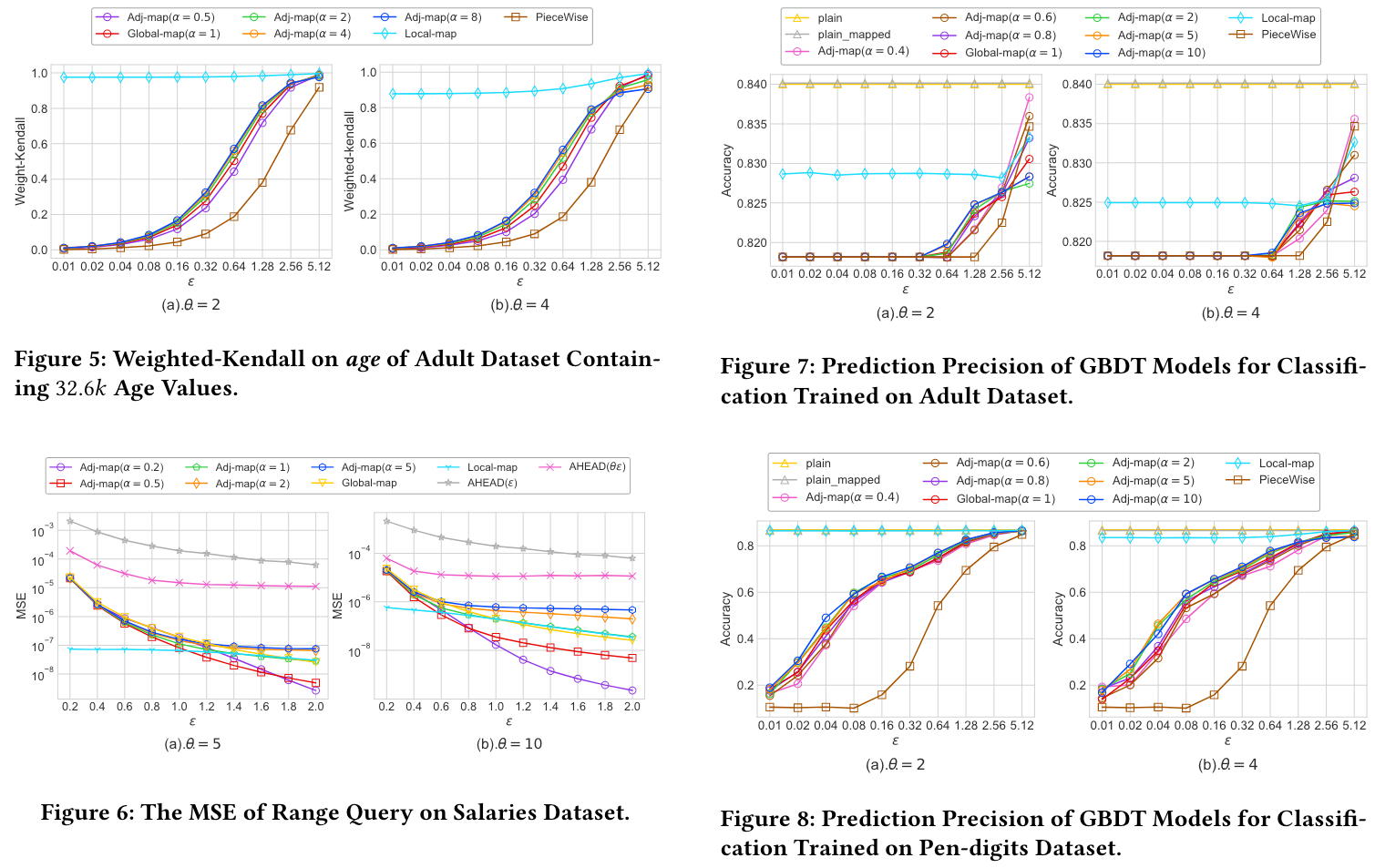
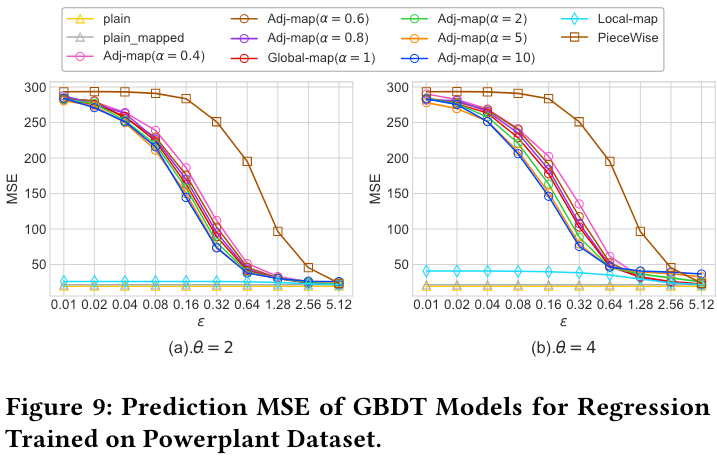
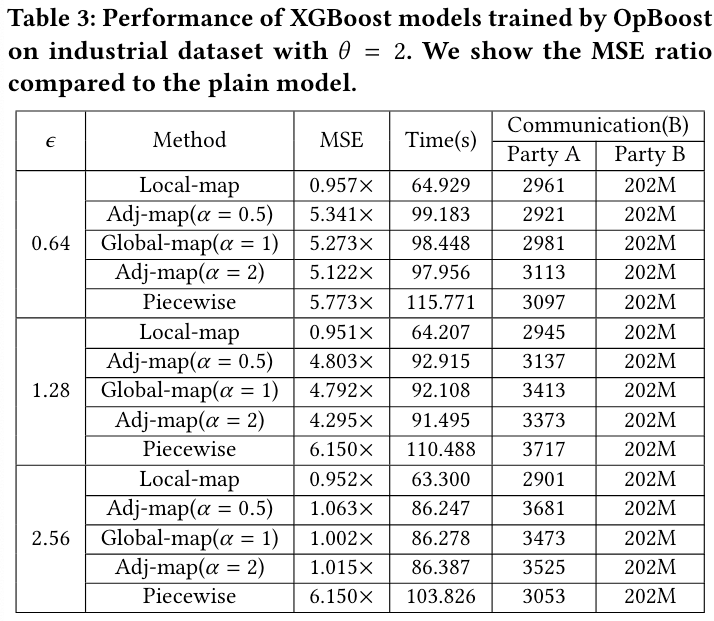
讨论
- 保序脱敏算法可以扩展到多特征值,利用组合定理将隐私预算分配给各个特征
- 对不关心不同分区中值的不可取分性的用户,Local-Map 是最佳选择
- 对没有额外领域知识,不追求高精度模型的用户,Global-Map 是最佳选择
- 对有额外领域知识和更高效用/精度追求的用户可以选择 Adj-Map,并自行设置 $ \alpha $ 和 $ \theta $
- 只有当 $ \epsilon $ 很大时(如 $ \epsilon > 2.56 $),$ \alpha < 1 $ 才占优
- 由于在实际应用中 $ epsilon $ 通常小于1甚至0.1,所以用户可以将 $ \alpha $ 一直保持在大于1的值
- 当 $ \alpha $ 过大时对结果并没有太大改善,所以没有必要将 $ \alpha $ 设置得过大