摘要
本篇文章定义了隐私保护任务规划(Privacy-Preserving Task Planning, PPTP)问题,该问题致力于任务位置的差分隐私和平台总收益最大化。本篇文章首先应用了拉普拉斯机制来保护位置,随后对 PPTP 问题提出了一种有效且高效的任务规划算法,并对其进行了验证。
介绍
本篇文章有如下贡献:
- 定义 PPTP 问题并提出一个高效的私有任务规划(Efficient Private Task Planning, EPTP)解决方案框架,其由一个可以保证地理不可区分性(geo-indistinguishability)的隐私机制和一个最大化收益的任务规划算法组成
- 量化了地理不可区分的隐私机制对任意任务规划算法的可靠性
- 在理论分析的基础上设计了一个新的任务规划算法,以较低的时间成本达到近似最大化收益
- 验证了算法的有效性和高效性
前言
本章定义了 PPTP 问题并提出了用于评估在位置隐私约束下的任务规划算法有效性的分析模型,下面是本章用到的符号说明:
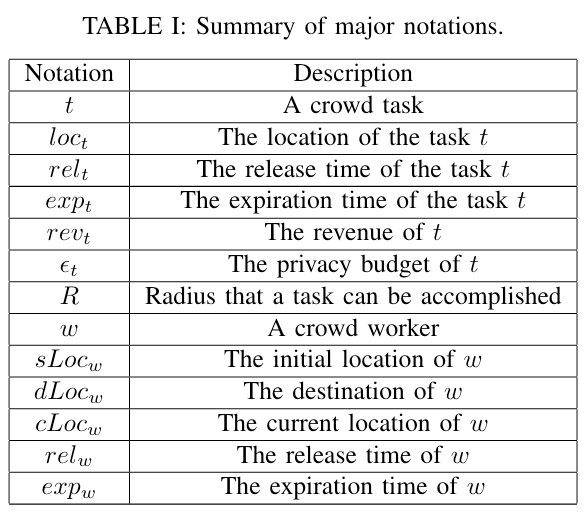
问题定义
任务(Task)
一个任务 $ t $ 是一个五元组 $ (loc_t, rel_t, exp_t, rev_t, \epsilon_t) $,其中 $ loc_t $ 是任务位置,$ rel_t $ 是释放时间,$ exp_t $ 是过期时间,$ rev_t $ 是任务 $ t $ 完成给平台带来的收入,$ \epsilon_t $ 是任务 $ t $ 的隐私预算。
考虑任务规划的在线设置,一个任务 $ t $ 的出现在释放时间 $ rel_t $ 之前是未知的。如果工人 $ w $ 在任务过期时间 $ exp_t $ 之前到达以 $ loc_t $ 为圆心,半径为 $ R $ 的圆内,则任务 $ t $ 完成。其中半径 $ R $ 定义在后文,取决于应用场合。
工人(Worker)
一个工人 $ w $ 是一个四元组 $ (sLoc_w, dLoc_w, rel_w, exp_w) $,其中 $ sLoc_w $ 是初始位置,$ dLoc_w $ 是目标位置,$ rel_w $ 是释放时间,$ exp_w $ 是过期时间。
一个工人 $ w $ 的出现在释放时间 $ rel_w $ 之前是未知的,工人在释放时间 $ rel_w $ 时出现在初始位置 $ sLoc_w $。使用 $ cLoc_w $ 来代替工人 $ w $ 的当前位置。如果一个工人 $ w $ 可以在有效时间间隔 $ [rel_t, exp_t] $ 内到达任务 $ t $ 的位置并处于圆心为 $ loc_t $,半径为 $ R $ 的圆内,则它可以完成这个任务 $ t $,并为平台增加 $ rev_t $ 的收入。此外,使用 $ dis(.,.) $ 来表示两个位置的距离,并假设工人以单位速度移动。
任务计划(Task Plan)
一个工人 $ w $ 的任务计划 $ p_w $ 是一个工人 $ w $ 从当前位置 $ cLoc_w $ 出发应该顺序到达的位置序列 $ \langle l_1, l_2, \dots, l_{\left|p_w\right|} \rangle $。当工人 $ w $ 可以在过期时间 $ exp_w $ 前到达目的地 $ dLoc_w $ 时这个计划 $ p_w $ 是合法的,即
$$ curT + dic(cLoc_w, l_1) + \sum_{i = 1}^{\left| p_w \right| - 1} dis(l_i, l_{i + 1}) \leq exp_w $$
其中 $ curT $ 是当前时间。
假设 $ P $ 是一个所有工人的计划集合,即 $ \{ p_w | w \in W \} $。由工人 $ w $ 完成的计划 $ p_w $ 定义为 $ AT(p_w) $。为了简便,使用 $ AT(P) $ 表示集合 $ P $ 中所有已完成的任务集合,即 $ A T(P)=\cup_{p \in P} A T(p) $。假设计划由任务规划算法生成,并保证有效性。
隐私机制(Privacy Mechanism)
给定一个位置空间 $ \mathcal{L} $ 和一个模糊位置空间 $ \mathcal{L}^\prime $,隐私机制 $ \mathcal{M} $ 是一个概率函数,将 $ \mathcal{L} $ 中的每个精确位置 $ x $ 以某种概率映射到 $ \mathcal{L}^\prime $ 中的一个模糊位置 $ x^\prime $
地理不可区分性(Geo-Indistinguishability)
一个隐私机制 $ \mathcal{M} $ 如果对任何 $ x_1, x_2 \in \mathcal{L} $ 和 $ x^\prime \in \mathcal{L}^\prime $ 有
$$ \frac{Pr(x_1, x^\prime)}{Pr(x_2, x^\prime)} \leq e^{\epsilon \cdot dis(x_1, x_2)} $$
则这个机制符合 $ \epsilon-Geo-Indistinguishability $
隐私保护任务规划问题(Privacy-Preserving Task Planning Problem, PPTP Problem)
给定一组动态工人集合 $ W $ 和一组动态任务集合 $ T $,问题是为任务设计一个隐私机制 $ \mathcal{M} $,为工人制定计划集合 $ P $,其中机制 $ \mathcal{M} $ 以任务 $ t $ 的位置 $ loc_t $ 为输入,输出一个符合地理不可区分性的模糊位置 $ loc_t^\prime $;并对任务的模糊位置进行规划,最大化已完成任务的总收益,即 $ Rev(P) = \sum_{t \in AT(P)} rev_t $,问题示例如下:
假设当前有2个工人和3个任务,他们的释放时间和过期时间如下 Table II 所示,对应的位置如下 Fig. 1 所示:
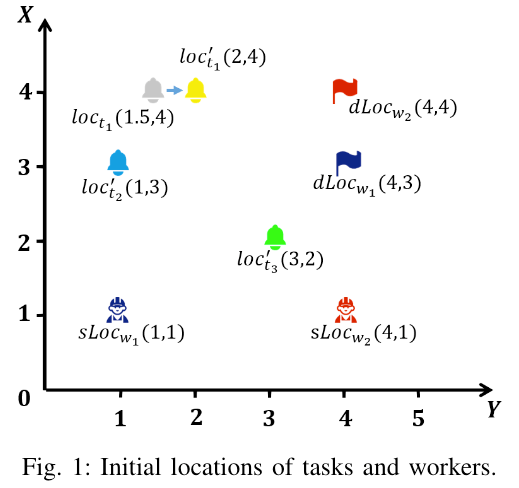
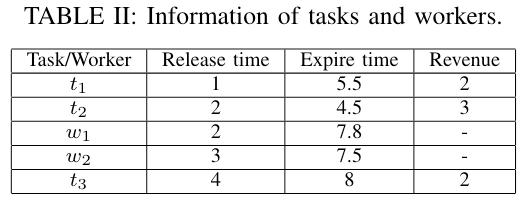
任务 $ t_1 $ 的真实位置 $ (1.5, 4) $ 被隐私机制扰动至模糊位置 $ (2, 4) $。假设半径 $ R $ 为1并且任务 $ t_1 $ 被分配给工人 $ w_1 $,因为 $ dis(t_1, t_1^\prime) = 0.5 \leq 1 $,所以工人 $ t_1 $ 可以通过到达模糊位置$ (2, 4) $ 来完成任务。
分析模型
竞争比(Competitive Ratio, CR)
假设 ALG 是基于混淆位置的兴趣算法,OPT 是基于任务精确位置的最优算法,ALG 的竞争比是在隐私机制分配的期望收益与 OPT 获得的收益之比,即
$$ C R_p(A L G)=\min _{I \in \mathcal{I}} \frac{\mathbb{E}_{\mathcal{M}}[\operatorname{Rev}(A L G(I))]}{\operatorname{Rev}(O P T(I))} $$
其中 $ \mathcal{I} $ 是所有实例的空间,$ ALG(I) $ 和 $ OPT(I) $ 是由 $ ALG $ 和 $ OPT $ 生成的规划。
高效的私有任务规划框架(Efficient Private Task Planning Framework, EPTP Framework)
框架概览
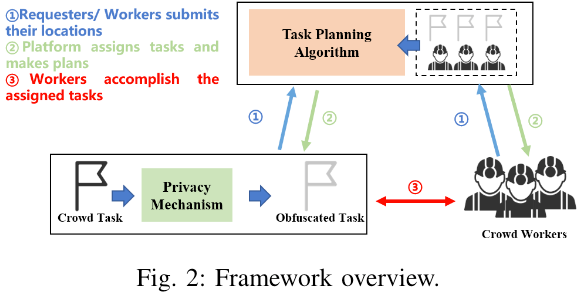
上图展示了 EPTP 框架的概览,工作流程如下:
- 平台收集工人和任务的信息,其中任务的精确位置在发送至平台之前使用隐私机制进行扰动
- 平台使用模糊位置来执行任务规划算法为工人制定计划
- 工人根据计划完成被指定的任务
隐私机制及分析
本文首先针对隐私预算为 $ \epsilon_t $ 的任务 $ t $ 提出了一种 $ \epsilon_t-geo-indistinguishability $ 的隐私机制,使用平面拉普拉斯分布,该机制将 $ loc_t \in \mathcal{X} $ 以下式的概率映射到 $ loc_t^\prime \in \mathcal{X} $:
$$ \operatorname{Pr}\left(l o c_t, l o c_t^{\prime}\right)=\frac{\epsilon_t^2}{2 \pi} \cdot e^{-\epsilon_t \cdot d i s\left(l o c_t, l o c_t^{\prime}\right)} $$
任务规划算法(Task Planning Algorithm)
本算法使用动态插入方法(dynamic insertion approach),在为单个工人规划时考虑了长期效应,并应用动态规划来提高算法的效率。动态插入方法描述如下:
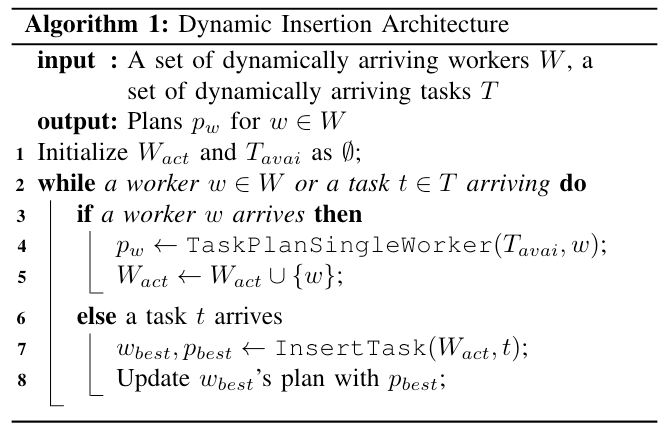
当一个工人 $ w $ 出现时,算法调用 TaskPlanSingleWorker 函数(在后文 Algorithm 2 中描述)来为 $ w $ 从可用任务集合 $ T_{avai} $ 中制定计划;当一个任务 $ t $ 出现时,算法调用 InsertTask 函数(在后文 Algorithm 3 中描述)以最小的额外距离将 $ t $ 插入到已经到达平台($ w_{best} \in W_{act} $)的工人的现有计划中,同时保持其他任务的顺序不变。
单工人任务规划(TaskPlanSingleWorker, Algorithm 2)
算法描述如下:

当为新出现的工人制定计划时使用贪心策略,通过下方两个定义来考虑当前的平均收益和长期效应。
-
每空移动距离收益(Revenue per Empty Moving Distance, REMD)
给定一个可用任务 $ t $ 和一个新出现的工人 $ w $,$ w $ 与 $ t $ 之间的 REMD 定义如下:
$$ R E(w, t)=\frac{\operatorname{rev}_t}{\operatorname{dis}\left(c \operatorname{Loc}_w, \operatorname{loc}_t^{\prime}\right)} $$
拥有更大 REMD 的任务在为新出现的工人分配任务时拥有较高的优先级。对于长期效应:- 如果任务 $ t $ 有较小的空闲时间($ exp_t - curT $),他应该被分配一个较高的优先级,因为它会以更高的概率过期
- 如果任务 $ t $ 更靠近 $ w $ 的目的地 $ dLoc_w $,它应当被分配较低的优先级,因为任务在之后(工人沿途前往目的地时)可以更有效的完成
为了衡量这种长期效应,定义了每一朝向目的地距离空闲时间(Spare Time per Heading Destination Distance, STHDD)
-
每一朝向目的地距离空闲时间(Spare Time per Heading Destination Distance, STHDD)
给定一个工人 $ w $ 和当前时间 $ curT $,$ w $ 与 $ t $ 之间的 STHDD 定义如下:
$$ S T(w, t)=\frac{\exp p_t-c u r T}{\operatorname{dis}\left(\operatorname{loc}_t^{\prime}, d L o c_w\right)} $$
不同于 REMD,拥有更大 STHDD 的任务意味着更低的优先级,因为它可以在之后更高效的完成。
上文 Algorithm 2 描述了考虑上述两方面(REMD, STHDD)的单工人任务规划算法,算法首先将可用任务集合 $ T_{avai} $ 根据 RMED 和 STHDD 的比值($ \frac{RE(w, t)}{ST(w, t)} $)进行排序,然后按排序顺序将任务追加到计划 $ p_w $ 中(只要任务不违反 $ t $ 和 $ w $ 的到期时间)。如果没有任务被分配给 $ w $,则 $ w $ 移动到它的目的地 $ dLoc_w $
基于动态规划的插入(Dynamic Programming based Insertion, Algorithm 3)
算法描述如下:

给定一个工人 $ w $ 和他未完成的计划 $ p_w = \langle l_1, l_2, \dots, l_{m_w} \rangle $,$ D_w[i] $ 是 $ w $ 从当前位置 $ cLoc_w $ 到第 $ i $ 个位置 $ l_i $ 所需的时间。在 $ p_w $ 中的最后一个位置也是 $ w $ 的目的地,即 $ l_{m_w} = dLoc_w $。对 $ i = 1, \dots, m_w $,$ E_w[i] $ 代表在第 $ i $ 个位置 $ l_i $ 之前插入任务 $ t^* $ 所引起的额外通行距离,即
$$ E_w[i] = \left\{\begin{array}{l}
\operatorname{dis}\left(c L o c_w, l o c_{t^*}^{\prime}\right)+\operatorname{dis}\left(l \operatorname{loc}_{t^*}^{\prime}, l_i\right)-\operatorname{dis}\left(c L o c_w, l_i\right), i=1 \\
\operatorname{dis}\left(l_{i-1}, l o c_{t^*}^{\prime}\right)+\operatorname{dis}\left(\operatorname{loc}_{t^*}^{\prime}, l_i\right)-\operatorname{dis}\left(l_{i-1}, l_i\right), 2 \leq i \leq m_w
\end{array}\right. $$
算法的基本思想是,如果我们将任务 $ t^* $ 插入到计划 $ p_w $ 中的位置 $ l_k $ 之前,则
- 对 $ 1 \leq i < k $,从 $ cLoc_w $ 到 $ l_i $ 的通行距离,即 $ D_w[i] $ 保持不变
- 对 $ k \leq i \leq m_w $,从 $ cLoc_w $ 到 $ l_i $ 的通行距离会增加 $ E_w[k] $
这表明当在 $ p_w $ 中寻找最佳的任务 $ t^* $ 的插入位置时,只有 $ E_w[k] $ 和 $ t^* $ 有关,其他变量都可以预先计算。更具体的,可以使用一个变量列表来代替在 $ p_w $ 中每个位置插入 $ t^* $ 的最大容忍的额外通行时间,并用这些变量来确定插入位置的有效性。设 $ MD_w[k] $ 为一个任务插入到 $ l_k $ 之前并保证所有 $ p_w $ 中的任务都不会过期的最大容忍额外通行时间,则 $ MD_w[k] $ 要么是任务在 $ l_k $ 的最大容忍额外通行时间(用 $ e_k $ 表示),形式表示为 $ e_k - D_w[k] $,要么是任务在 $ \{l_{k+1}, l_{k+2}, \dots, l_{m_w}\} $ 的最大容忍额外通行时间。
因此,我们可以用如下的方法计算 $ MD_w[k] $:
$$ M D_w[k]= \begin{cases}\exp _w-D_w\left[m_w\right], & k=m_w \\ \min \left(e_k-D_w[k], M D_w[k+1]\right), & 1 \leq k<m_w\end{cases} $$
在计算出 $ 1 \leq k \leq m_w $ 的 $ MD_w[k] $ 后,我们可以通过判断是否 $ E_w[k] \leq MD_w[k] $ 来确定任务 $ t $ 在 $ t_k $ 之前的插入是否合法(不会导致过期)。最后我们可以通过从 $ m_w $ 到 1 迭代 $ k $,计算 $ MD_w[k] $ 和 $ E_w[k] $,并比较是否 $ E_w[k] \leq MD_w[k] $ 来寻找最佳插入位置。
为了找到最佳插入位置,对每个工人 $ w_a \in W_{act} $,首先基于上文提到的算式计算列表 $ E_{w_a}[.] $ 和 $ MD_w[.] $,随后对每个插入位置 $ i $,对 $ E_{w_a}[i] $ 和 $ MD_{w_a}[i] $ 的值进行对比来判断插入后的计划是否有效且有最小的额外距离,并更新当前最佳插入位置。
实验
本文在合成和真实数据集上进行了实验,实验参数如下表:
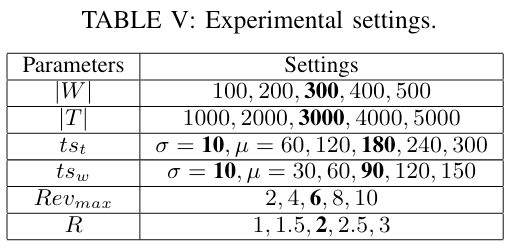
本文将 EPTP 与两种具有相同隐私机制的先进任务规划算法进行了比较:
- baseline-Delay:Delay Planning algorithm,为每个新到达的工人分配任务,并保持计划不变直到工人完成计划
- baseline-Fast:Fast Planning algorithm,随着任务到来不断更新计划
实验结果如下:
任务数量和工人数量的影响(Effect of $ \left| T \right| $ && Effect of $ \left| W \right| $)
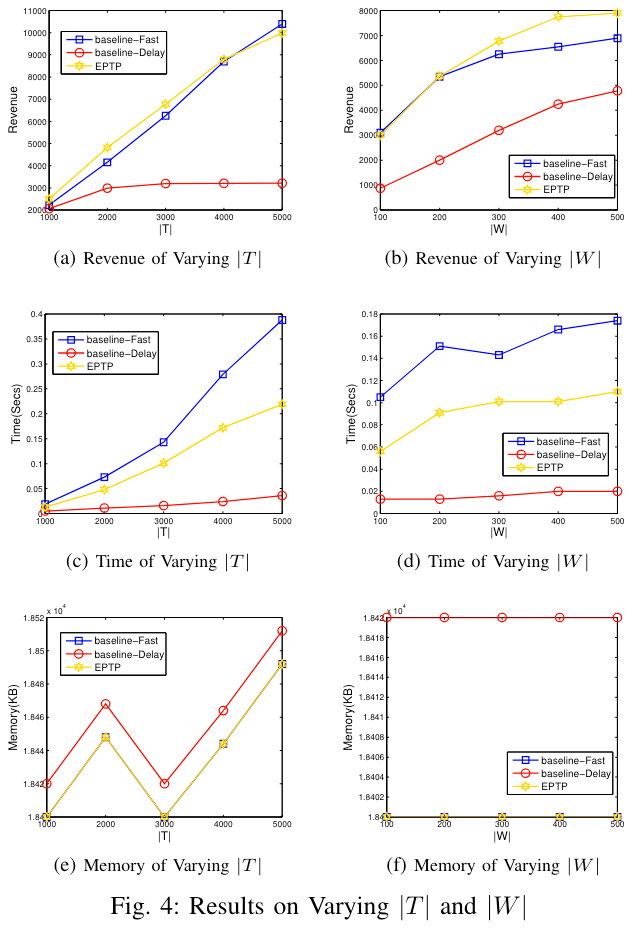
当工人数量不变时,EPTP 表现最好,其次是 baseline-Fast,最后是 baseline-Delay,这是因为 EPTP 考虑了当前收入和长期效应。
当任务数量不变时,随着工人数量的增加,所有三种算法(包括EPTP)的收入都会增加。其中,EPTP 在大多数情况下表现最佳,并且相对于 baseline 有39%-70%的收入提高。此外,随着工人数量的增加,baseline-Fast 和 EPTP 的时间成本也会增加,而 baseline-Delay 则保持稳定。最后,在内存成本方面,EPTP 和 baseline-Fast 消耗相似大小的内存,并且它们在内存成本方面更有效率。
任务空闲时间($ exp_t - rel_t $)和工人空闲时间($ exp_w - rel_w $)的影响(Effect of $ ts_t $ && Effect of $ ts_w $)
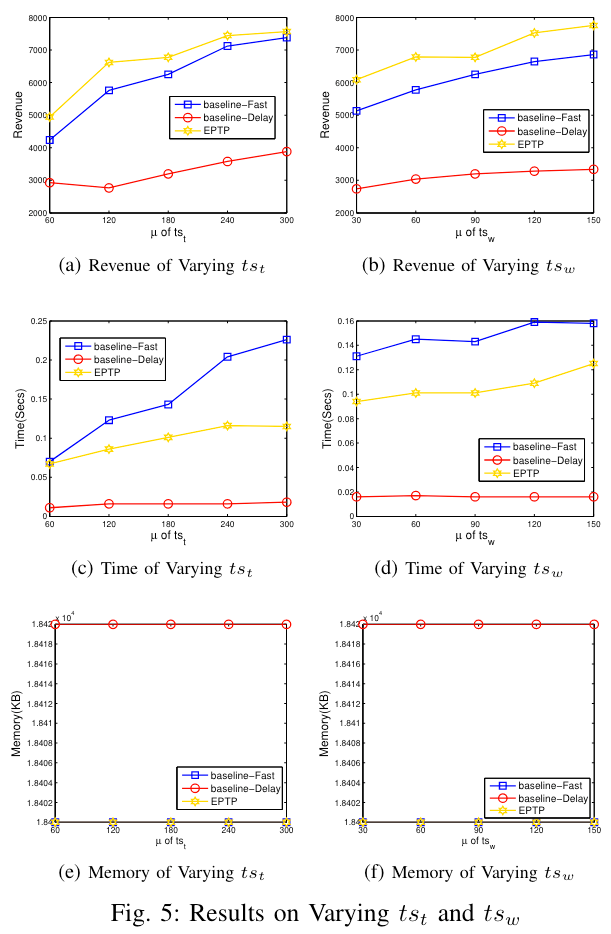
在不同任务空闲时间的情况下,EPTP 仍然是最优的。随着任务空闲时间的增加,三种算法的收入都增加,但是 baseline-Delay 的收入较小。在时间方面 baseline-Fast 和 EPTP 都会增加,baseline-Delay 保持不变。
在不同工人空闲时间的情况下,EPTP 还是最优的。随着任务空闲时间的增加,三种算法的收入都增加,EPTP 收入最高。在时间方面,在大多数情况下所有算法的时间成本保持稳定,这是因为无论如何算法都要遍历所有任务,所以时间不会有太大改变。/
半径 $ R $ 和最大收入的影响(Effect of the radius $ R $ && Effect of $ Rev_{max} $)

在不同半径 $ R $ 的情况下,EPTP 在大多数情况下仍然表现最好。随着半径增加,三种算法收益都增加。在时间成本上,EPTP 优于 baseline-Fast,baseline-Delay 表现最优。
在不同最大收益的情况下,EPTP 仍然优于 baseline,所有算法的收益都随着 $ Rev_{max} $ 的增加而增加。baseline-Fast 和 EPTP 的增加幅度大于 baseline-Delay。时间和内存成本稳定。
在真实数据集上的表现(Performance on Real Datasets)
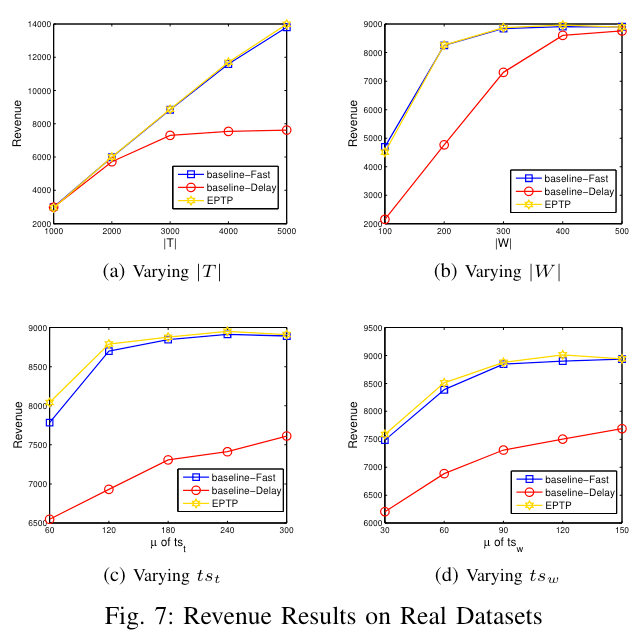
EPTP 在大多数情况下优于 baseline,并拥有合理的时间和内存开销,与合成数据集上的实验结果一致。