VLDB22 Federated Matrix Factorization with Privacy Guarantee

摘要

本文主要研究了不同联邦学习环境下的矩阵分解（MF）问题，提出了一个通用的联邦矩阵分解（FMF）算法框架，系统地表征了垂直联邦学习（VFL）、水平联邦学习（HFL）和本地联邦学习（LFL）三种不同设置的数据采集、训练和发布阶段的隐私泄露风险，并引入隐私概念和一种新的被称为嵌入裁剪的私有学习技术以提供端到端的隐私保护。

介绍

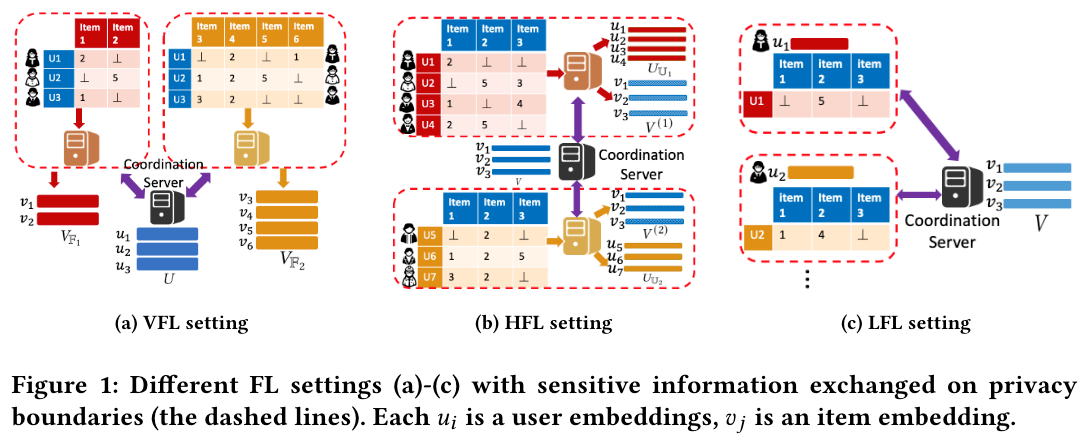
本章主要介绍了一些联邦学习的概念和三种不同设置的联邦学习（VHL、HFL、LFL）所需要的不同的隐私边界设置。

本文的贡献如下：

• 提出了一个应用于三种设置的抽象的计算范式
• 针对不同的隐私泄露风险为不同的设置设计了不同的 FL 算法
• 提出使用嵌入裁剪（Embeddings Clipping）代替梯度裁剪（Gradient Clipping）来进行更新
• 提出了用于矩阵分解的 SGDMF 算法（包括 VFL-SGDMF、HFL-SGDMF、LFL-SGDMF）

背景

本章主要介绍了一些背景知识，如矩阵分解、差分隐私等

矩阵分解

矩阵分解问题可以形式化为如下最小化损失函数：
$$\mathcal{L}(X,U,V):\frac{1}{|\mathrm{\Omega }|}\sum _{(i,j)\in \mathrm{\Omega }}{\mathcal{L}}_{i,j}(X,U,V)=\frac{1}{|\mathrm{\Omega }|}\sum _{(i,j)\in \mathrm{\Omega }}(X_{ij}-⟨u_i,{\nu }_j⟩{)}^2$$

差分隐私

• Sequential composition: moments accountant
  $M(X,aux)$ 表示 $X$ 的输出，$aux$ 为辅助输入，可包含前面步骤的所有中间结果
  在 $\lambda$ 处的矩生成函数（$M$ 中的隐私损失）的对数定义如下：
  $${\alpha }_M(\lambda ;X,X^{\prime },aux)=log{E}_{oM(X,aux)}[exp(\lambda log\frac{Pr[M(X,aux)=o]}{Pr[M(X^{\prime },aux)=o]})]$$
  其中上界为 ${\alpha }_M(\lambda )=ma{x}_{X,X^{\prime },aux}{\alpha }_M(\lambda ;X,X^{\prime },aux)$，$M_t$ 为适应性机制，使用 $M_1{M}_{t-1}$ 和数据集 $X$ 作为输入
  Moments Accountant 将总体隐私损失限制在 $M_1$ 到 $M_T$ 之间（通过 $log$ 矩母函数）

• Moments Accountant
  设机制 $M$ 为一系列适应性机制 $M_1,\dots ,M_T$，则有
  (1) 对任何 $\lambda$，有 ${\alpha }_M(\lambda )\le \sum _{t=1}^T{\alpha }_{M_t}(\lambda )$
  (2) 对任何 $ϵ>0$，机制 $M$ 为 $(ϵ,\delta )$ - 差分隐私，$\delta =mi{n}_{\lambda }exp({\alpha }_M(\lambda )-{\lambda }_{ϵ})$

• Parallel Composition
  若 $M_1,\dots ,M_T$ 为 $({ϵ}^{(1)},{\delta }^{(1)}),\dots ,({ϵ}^{(s)},{\delta }^{(s)})$ - 差分隐私，且他们都在不相交的数据集 $X_1,\dots ,X_s$ 上计算，则整体隐私损失为 $(ma{x}_k\{{ϵ}^{(k)}\},ma{x}_k\{{\delta }^{(k)}\})$

• Per-rating Privacy
  当有一索引 $(i,j)$ 使得 $X_{i,j}=\perp$ 且 $X_{i,j}^{\prime }\ne \perp$（或相反），且对任意 $(i^{\prime },j^{\prime })\ne (i,j)$，有 $X_{i^{\prime },j^{\prime }}=X_{i,j}$，则 $X,X^{\prime }$ 为相邻数据集
  Per-rating Privacy 保护每个单独的由每个用户给出的评分

• Bounding Sensitivity
  Sensitivity 指的是当数据有一条发生变化（增加 / 删除）时所产生的影响

• Gradient Clipping
  梯度裁剪可以用于 Bounding Sensitivity，但是在实际应用中有限制每个评分的效果和需要额外空间存储每个评分梯度的问题

• Trimming
  限制参与方 $k$ 的最大评分数为 ${\theta }^{(k)}$，并将剩余评分转换为 $\perp$

联邦矩阵分解

本章介绍了在三种不同设置（VFL、HFL、LFL）下的矩阵分解

垂直联邦学习（VFL）下的矩阵分解

User embeddings $U=[u_i{]}_{i\in [n]}\in {\mathbb{R}}^{n\times p}$

Item embeddings $V_{{\mathbb{F}}_k}=[{\nu }_i{]}_{j\in {\mathbb{F}}_k}\in {\mathbb{R}}^{m_k\times p}$

对参与方 $k$ 的损失函数：$\mathcal{L}({\mathrm{X}}_{{\mathbb{F}}_k},U,V_{{\mathbb{F}}_k})=\frac{1}{\left|{\mathrm{\Omega }}_k\right|}\sum _{(i,j)\in {\mathrm{\Omega }}_k}{({\mathrm{X}}_{ij}-⟨u_i,v_j⟩)}^2$

整体损失函数：$\mathcal{L}(\mathrm{X},U,V)=\sum _k\frac{\left|{\mathrm{\Omega }}_k\right|}{|\mathrm{\Omega }|}\mathcal{L}({\mathrm{X}}_{{\mathrm{F}}_k},U,V_{{\mathrm{F}}_k})=$ $\frac{1}{|\mathrm{\Omega }|}\sum _k\sum _{(i,j)\in {\mathrm{\Omega }}_k}{({\mathrm{X}}_{ij}-⟨u_i,v_j⟩)}^2$

User Embeddings：${\mathrm{\nabla }}_U\mathcal{L}(\mathrm{X},U,V)=\sum _k\frac{\left|{\mathrm{\Omega }}_k\right|}{|\mathrm{\Omega }|}{\mathrm{\nabla }}_U\mathcal{L}({\mathrm{X}}_{{\mathbb{F}}_k},U,V_{{\mathbb{F}}_k})$

Item Embeddings：${\mathrm{\nabla }}_{V_{{\mathbb{F}}_k}}\mathcal{L}(\mathrm{X},U,V)=\frac{\left|{\mathrm{\Omega }}_k\right|}{|\mathrm{\Omega }|}{\mathrm{\nabla }}_{V_{{\mathbb{F}}_k}}\mathcal{L}({\mathrm{X}}_{{\mathbb{F}}_k},U,V_{{\mathbb{F}}_k})$

User Embaddings 的归一化随机梯度：${\mathrm{g}}_U^{(k)}=\frac{1}{n^{\prime }{m}_k^{\prime }\tau }\sum _{(i,j)\in I_k}{\mathrm{\nabla }}_U{\mathcal{L}}_{i,j}({\mathrm{X}}_{{\mathrm{F}}_k},U^{(k)},V_{{\mathrm{F}}_k})\approx {\mathrm{\nabla }}_U\mathcal{L}({\mathrm{X}}_{{\mathrm{F}}_k},U,V_{{\mathrm{F}}_k})$

Item Embaddings 的归一化随机梯度：${\mathrm{g}}_{V_{{\mathrm{F}}_k}}^{(k)}=\frac{1}{n^{\prime }{m}_k^{\prime }\tau }\sum _{(i,j)\in I_k}{\mathrm{\nabla }}_{V_{{\mathrm{F}}_k}}{\mathcal{L}}_{i,j}({\mathrm{X}}_{{\mathrm{FF}}_k},U^{(k)},V_{{\mathrm{F}}_k})\approx {\mathrm{\nabla }}_{V_{{\mathrm{F}}_k}}\mathcal{L}({\mathrm{X}}_{{\mathrm{F}}_k},U,V_{{\mathrm{F}}_k})$

水平联邦学习（HFL）下的矩阵分解

局部损失函数：$\mathcal{L}({\mathbf{X}}_{{\mathbb{U}}_k},U_{{\mathbb{U}}_k},V)=\frac{1}{\left|{\mathrm{\Omega }}_k\right|}\sum _{(i,j)\in {\mathrm{\Omega }}_k}{({\mathbf{X}}_{ij}-⟨u_i,v_j⟩)}^2$

全局损失函数：$\mathcal{L}(\mathrm{X},U,V)=\sum _k\frac{\left|{\mathrm{\Omega }}_k\right|}{|\mathrm{\Omega }|}\mathcal{L}({\mathrm{X}}_{{\mathbb{U}}_k},U_{{\mathbb{U}}_k},V)$

本地联邦学习（LFL）下的矩阵分解

LFL 是一种当 $s=n,{\mathbb{U}}_i=\{i\}$ 时的 HFL 特例

MF 问题常用的 FL 范式

1. 初始化和局部预计算
2. 联合学习（需要通信）
3. 局部微调

在 VFL 中，share embedding 是 user embedding，而在 HFL 中，share embedding 是 item embedding

在上述三个步骤中，步骤 1、3 可以在本地完成，而步骤 2 需要通信，更新步骤如下：

VFL：$U^{(k)}\leftarrow U^{(k)}-{\gamma }_t{\mathrm{g}}_U^{(k)},V_{{\mathbb{F}}_k}\leftarrow V_{{\mathbb{F}}_k}-\frac{{\gamma }_t{m}_k}{m}{\mathbf{g}}_{V_{{\mathbb{F}}_k}}^{(k)}$

HFL： $U_{{\mathbb{U}}_k}\leftarrow U_{{\mathbb{U}}_k}-\frac{{\gamma }_t{n}_k}{n}{\mathbf{g}}_{U_{{\mathbb{U}}_k}}^{(k)},V^{(k)}\leftarrow V_{{\mathbb{F}}_k}-{\gamma }_t{\mathbf{g}}_{V^{(k)}}^{(k)}$

算法描述如下 Figure 3：

隐私垂直联邦学习矩阵分解 VFL-SGDMF

Embedding Clipping

因为所有评分都在 $[0,R]$ 的范围内（$R$ 是一个有限的数字），所以 user embeddings 和 item embeddings 都被限制为非负的，所以在本文中对 user embeddings 和 item embeddings 施加了更强的约束如下：

$$\mathcal{U}:\mathrm{\forall }i\in [n],{\Vert u_i\Vert }_2^2\le R,u_i\ge 0,\mathcal{V}:\mathrm{\forall }j\in [m],{\Vert v_j\Vert }_2^2\le R,v_j\ge 0$$

Random Trimming

对每个参与方 $k$，将其局部数据集中每个用户所拥有的评分数限制在 ${\theta }^{(k)}$，并将其余评分转换为 $\perp$

隐私放大

通过使用 mini-batch 技术可实现隐私放大，对数据进行采样

隐私局部更新

为了保护中间和最终结果，$U$ 和 $V$ 都需要加入一个随机的噪声进行扰动，并且投影到上文 Embedding Clipping 中所提到的约束域

局部更新 U：$U^{(k)}={\mathrm{\Pi }}_{\mathcal{U}}(U^{(k)}-{\gamma }_t{\tilde{\mathrm{g}}}_U^{(k)})$

局部更新 V：$V_{{\mathbb{F}}_k}={\mathrm{\Pi }}_{\mathcal{V}}(V_{{\mathbb{F}}_k}-\frac{{\gamma }_t{m}_k}{m}{\tilde{\mathrm{g}}}_{V_{{\mathbb{F}}_k}}^{(k)})$

其中 ${\tilde{\mathrm{g}}}_U^{(k)}={\mathrm{g}}_U^{(k)}+{\xi }_U^{(k,t,t^{\prime })}$，${\tilde{\mathrm{g}}}_{V_{{\mathrm{F}}_k}}^{(k)}={\mathrm{g}}_{V_{{\mathrm{F}}_k}}^{(k)}+{\xi }_{V_{{\mathrm{F}}_k}}^{(k,t,t^{\prime })}$，噪音 ${\xi }_U^{(k,t,t^{\prime })}$ 和 ${\xi }_{V_{{\mathbb{F}}_k}}^{(k,t,t^{\prime })}$ 的维度和梯度的，且对于每个局部更新，它们独立于零均值高斯分布进行采样，方差取决于隐私定义和隐私参数

VFL-SGDMF 局部微调

VFL-SGDMF 算法的收敛取决于两方面：DP 噪声和问题的非凸性

对最后的 $\kappa$ 轮迭代，user embeddings 是固定的，各参与方只更新 item embeddings，最终每个参与方在训练时访问局部评分矩阵 $TT\prime +\kappa$ 次。由于在最后的迭代中只有 item embeddings 发生变化，所以每次局部更新的敏感度较小。将问题转化为凸问题，每次更新的噪声更小，可以在训练中获得更小更稳定的损失。

隐私水平联邦学习矩阵分解 HFL-SGDMF

1. 初始化和局部预计算
2. 联合学习
   每个参与方使用差分隐私保护更新本地 item embeddings：$V^{(k)}={\mathrm{\Pi }}_{\mathcal{V}}(V^{(k)}-{\gamma }_t{\tilde{\mathbf{g}}}_V^{(k)})$，其中 ${\tilde{\mathbf{g}}}_V^{(k)}$ 是采样率为 $\eta =\frac{n_k\prime }{n_k}$ 和固定 $U_{{\mathbb{U}}_k}$ 的 item embeddings 的 mini-batch 的隐私梯度。
3. 局部微调

跨设备学习：LFL-SGDMF

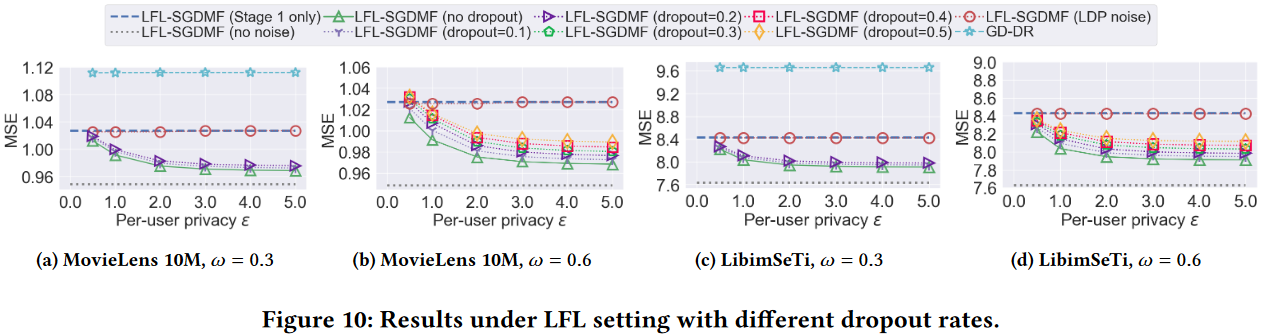
不同于 HFL，LFL 可能会面临用户设备不可用或用户设备与中心方之间的通信断开的情况，所以需要保证在训练过程中即使有大量用户在一次或多次迭代中退出的情况下 LFL 仍然可以可以保证隐私性。

LFL-SGDMF 改编自 FMF 算法，主要对第二步联合学习进行了修改，基本思想是在通过 SA（Secure Aggregation）聚合 item embeddings 的更新的同时保证聚合梯度满足 DP，同时引入尽可能小的噪声。

如果将 SA 看作一个预言机，则在每轮迭代中都会有两轮通信。

• 第一轮通信
  协调服务器发起 $S{A}_{\omega }$，并从各参与方请求更新。对每个参与方 $i$ 进行一次采样 $X_{ij}$，并报告更新噪声为 ${\tilde{\mathrm{g}}}_V^{(i,t)}={\mathrm{\nabla }}_V{\mathcal{L}}_{i,j}(u_i,V^{(t)})+{\xi }^{(i,t)}$，其中噪声 ${\xi }^{(i,t)}$ 取样自高斯分布 $(0,{\zeta }_1{\sigma }_v^2)$。随后参与方调用预言机 ${\mathrm{SA}}_{\omega }-\mathrm{report}\left({\tilde{\mathrm{g}}}_V^{(i,t)}\right)$，服务器通过调用 $S{A}_{\omega }-agg$ 对上报的更新进行聚合。本轮的幸存者集合记为 ${\mathbb{U}}^{(t,1)}$。若剩余用户量小于 $(1-\omega )n$，则 $S{A}_{\omega }$ 中止，本轮没有学习到任何东西，反之由 $S{A}_{\omega }$ 解码的聚合梯度可以被分解为 ${\tilde{\mathrm{g}}}_V^{(t)}=\sum _{i\in {\mathbb{U}}^{(t,1)}}{\mathrm{\nabla }}_V{\mathcal{L}}_{i,j}(u_i,V^{(t)})+\sum _{i\in {\mathbb{U}}^{(t,1)}}{\xi }^{(i,t)}$

• 第二轮通信
  协调服务器首先向幸存者广播 $|{\mathbb{U}}^{(t,1)}|$ 并请求替换噪声。存活的参与方向协调服务器发送 ${\overline{\xi }}^{(i,t)}=-{\xi }^{(i,t)}+{\xi }^{\prime (i,t)}$，其中 ${\xi }^{\prime (i,t)}$ 取样自高斯分布 $(0,{\zeta }_2{\sigma }_v^2)$。用户退出也可能发生在第二轮，所以记第二轮的幸存者集合为 ${\mathbb{U}}^{(t,2)}$。服务器对替换噪声进行聚合，将两轮交换后的聚合噪声梯度分解为 ${\tilde{\mathrm{g}}}_V^{(t)}=\sum _{i\in {\mathbb{U}}_t}{\mathrm{\nabla }}_V{\mathcal{L}}_{i,j}(u_i,V^{(t)})+\sum _{i\in {\mathbb{U}}^{(t,1)}-{\mathbb{U}}^{(t,2)}}{\xi }^{(i,t)}+\sum _{i\in {\mathbb{U}}^{(t,2)}}{\xi }^{\prime (i,t)}$，协调服务器利用这些信息更新 item embeddings，并将更新后的值广播给各方。

LFL-SGDMF 对每个参与方的通信成本为 $O(T(logn+mp))$